Ypologismos.gr Life of Numbers
Υπολογισμός ύψους του ρόμβου με 3 διαφορετικούς τρόπους. Μαθηματικοί τύποι εύρεσης του ύψους στον ρόμβο. Διαγώνιοι, πλευρές, γωνίες. Ιδιότητες - Κρητήρια
Υπολογισμός ύψους ρόμβου online
Height of Rhombus online calculator – calculation
1 Υψος ρόμβου γνωρίζοντας την πλευρά (a) και μοίρες γωνίας
Υψος ρόμβου (h) γνωρίζοντας την πλευρά (a) και τις μοίρες της γωνίας (Α) ή (C)
2 Υψος ρόμβου γνωρίζοντας πλευρά (a) και μοίρες γωνίας (B) ή (D)
Υψος ρόμβου (h) γνωρίζοντας την πλευρά (a) και τις μοίρες της γωνίας (B) ή (D)
3 Υψος ρόμβου γνωρίζοντας το μήκος των διαγώνιων
Υψος ρόμβου (h) γνωρίζοντας το μήκος των διαγώνιων του (p & q)
Ύψος ρόμβου, μαθηματικός τύπος
Μπορείτε να υπολογίσετε το ύψος ενός ρόμβου, χρησιμοποιώντας έναν από τους τρεις κάτωθι τύπους, όπου :
1. Εύρεση ύψους ρόμβου (h) – πλευρά (a) και τις μοίρες της γωνίας (Α) ή (C)
Υπολογίστε το ύψος ενός ρόμβου h, αν γνωρίζετε το μήκος των διαγωνίων p και q, χρησιμοποιώντας τον κάτωθι μαθηματικό τύπο :
$$ h = a · sin (A)$$και όπου sin(A) είναι το ημίτονο της γωνίας Α
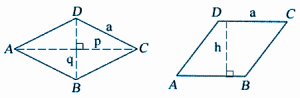
2. Γνωρίζοντας την πλευρά (a) και τις μοίρες της γωνίας (B) ή (D)
Υπολογίστε το ύψος ενός ρόμβου h, αν γνωρίζετε το μήκος το μήκος της πλευράς a και το ύψος h, χρησιμοποιώντας τον κάτωθι μαθηματικό τύπο :
$$ h = a · sin (B)$$και όπου sin(B) είναι το ημίτονο της γωνίας B
3. Γνωρίζοντας το μήκος των διαγώνιων του (p & q)
Υπολογίστε το ύψος ενός ρόμβου h, αν γνωρίζετε το μήκος της πλευράς a και την γωνία A ή C χρησιμοποιώντας τον κάτωθι μαθηματικό τύπο :
$$h = (p · q)/(2 · a) $$όπου πλευρά ρόμβου (a) είναι δίδεται από τον τύπο
$$ a= √{(p^2 + q^2)/4}$$όπου για τις 3 παραπάνω μαθηματικούς τύπου, ισχύουν τα εξής :
- a = η κάθε πλευρά ρόμβου (ίσες μεταξύ τους)
- p και q = διαγώνιοι ρόμβου (p του μεγάλου άξονα και q του μικρού άξονα)
- h = ύψος ρόμβου
- A, B, C, D = οι γωνίες του ρόμβου (A = C και B = D σε μοίρες)
- K = εμβαδόν επιφάνειας ρόμβου
- P = περίμετρος ρόμβου
- sin(A) = ημίτονο της γωνίας Α (ανάλογα και για άλλες γωνίες A,C,B,D)
- π = pi = 3,14159
- √ = τετραγωνική ρίζα
Ρόμβος – Rhombus
Ιδιότητες
- Σε έναν ρόμβο όλες οι πλευρές είναι ίσες.
- Σε κάθε ρόμβο, οι διαγώνιοι τέμνονται κάθετα, διχοτομούν τις γωνίες του και είναι άξονες συμμετρίας του.
Κριτήρια ρόμβου
Ένα τετράπλευρο είναι ρόμβος αν και μόνο αν ισχύει μία από τις παρακάτω προτάσεις:
- Έχει όλες τις πλευρές του ίσες.
- Είναι παραλληλόγραμμο με δύο διαδοχικές πλευρές ίσες.
- Είναι παραλληλόγραμμο με κάθετες διαγωνίους.
- Είναι παραλληλόγραμμο με μία διαγώνιο να διχοτομεί γωνία του.
- Υπολογισμός εμβαδού σε ρόμβο. Διαγώνιοι, πλευρά, ύψος, γωνίες ρόμβου
- Υπολογισμός πλευρές ρόμβου. 4 τρόποι εύρεσης μήκους πλευρών σε ρόμβο
- Υπολογισμός διαγώνιοι ρόμβου. Βες το μήκος διαγωνίων στον ρόμβο.
- Υπολογισμός περιμέτρου ρόμβου. Άθροισμα μήκους πλευρών στον ρόμβο
- Υπολογισμός ύψους ρόμβου με 3 τρόπους. Διαγώνιοι, πλευρές, γωνίες
