Πίνακες Πολλαπλασιασμός. Υπολογισμός πολλαπλασιασμού των στοιχείων - εγγραφών δύο Πινάκων m γραμμών και n στηλών. Matrix Multiplication Calculator online
Πολλαπλασιασμός των στοιχείων δύο Πινάκων m γραμμών και n στηλών
Matrix Multiplication Calculator online
Πολλαπλασιάστε online τα στοιχείων – εγγραφές δύο Πινάκων Α και Β online.
Πίνακας – Μαθηματικά – Γραμμική Άλγεβρα
ή με πιο απλή διατύπωση
Μια διάταξη μ • ν το πλήθος αριθμών σε μορφή ορθογωνίου σχήματος με μ γραμμές και ν στήλες, λέγεται πίνακας τύπου μ x ν ή απλούστερα μ x ν πίνακας.
Η γραμμική άλγεβρα μελετάει τις ιδιότητες ενός πίνακας Α, δηλαδή ενός συνόλου αριθμών τοποθετημένων σε m γραμμές και n στήλες. Οι αριθμοί m, n καθορίζουν τη διάσταση γραμμών και στηλών, αντίστοιχα. Επιπρόσθετα, όταν m = n αρκεί να αναφερόμαστε (συνολικά) στη διάσταση του πίνακα.
Ένα παράδειγμα πίνακα 2 γραμμών και 3 στηλών είναι:
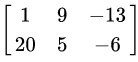
Οι πίνακες ίδιων διαστάσεων μπορούν να προστεθούν ή αφαιρεθούν στοιχείο προς στοιχείο.
Μια σημαντική εφαρμογή των πινάκων είναι να παριστάνουν γραμμικούς μετασχηματισμούς, δηλαδή, γενικεύσεις των γραμμικών συναρτήσεων όπως f(x) = 4x.
Διαστάσεις Πινάκων
Η διάσταση ενός πίνακα ορίζεται από τον αριθμό των γραμμών και στηλών που περιέχει. Ένας πίνακας με m γραμμές και n στήλες ονομάζεται m × n πίνακας ή m-επί-n πίνακας, ενώ τα m και n ονομάζονται διαστάσεις του.
Σε μερικά περιβάλλοντα όπως στα προγράμματα υπολογιστικής άλγεβρας είναι εύχρηστο να σκεφτούμε έναν πίνακα χωρίς γραμμές ή χωρίς στήλες, που ονομάζεται ”άδειος πίνακας”.
Συμβολισμός Πινάκων. Αγκύλες, στήλες, εγγραφές
Οι πίνακες είναι συνήθως γραμμένοι σε αγκύλες:

Ένας εναλλακτικός συμβολισμός χρησιμοποιεί μεγάλες παρενθέσεις αντί για αγκύλες:

Οι ιδιαιτερότητες στο συμβολισμό ενός συμβολικού πίνακα ποικίλουν ευρέως, με μερικές επικρατούσες τάσεις. Οι πίνακες συνήθως συμβολίζονται χρησιμοποιώντας κεφαλαία γράμματα (όπως A στο παραπάνω παράδειγμα), ενώ τα αντίστοιχα πεζά γράμματα, με δύο δείκτες (π.χ., a11, ή a1,1), αντιπροσωπεύουν τις εγγραφές | via
Ίσοι Πίνακες Α=Β
Δύο πίνακες Α=(aij) και Β =( bij) θα λέμε ότι είναι ίσοι, και θα γράφουμε Α=Β, εάν καταρχάς οι δύο πίνακες έχουν τις ίδιες διαστάσεις και επιπλέον τα αντίστοιχα στοιχεία τους είναι ίσα, με άλλα λόγια αν
aij=bij για όλα τα i,j
Εναλλακτική διατύπωση: Δυο A, B πίνακες λέμε ότι είναι ίσοι, όταν έχουν τον ίδιο αριθμό γραμμών, τον ίδιο αριθμό στηλών (δηλαδή αν είναι του ίδιου τύπου) και τα αντίστοιχα στοιχεία τους είναι ίσα. Για να δηλώσουμε ότι δύο πίνακες είναι ίσοι γράφουμε A = B
Από τον ορισμό αυτό προκύπτει ότι δύο πίνακες διαφορετικού τύπου δεν μπορεί να είναι ίσοι.
Τετραγωνικός πίνακας – Πίνακας γραμμή ή στήλη
Αν ένας πίνακας έχει τον ίδιο αριθμό γραμμών και στηλών, δηλαδή είναι τύπου ν x ν τότε ο πίνακας αυτός λέγεται τετραγωνικός πίνακας.
Πίνακες οι οποίοι έχουν μία μόνη γραμμή λέγονται διανύσματα γραμμής ή πίνακας γραμμή, και εκείνοι οι οποίοι έχουν μία μόνη στήλη ονομάζονται διανύσματα στήλης ή πίνακας στήλη.
Ένας πίνακας με άπειρο αριθμό γραμμών ή στηλών (ή και τα δύο) ονομάζεται «άπειρος πίνακας»
Πίνακας τριγωνικός άνω και τριγωνικός κάτω
Ένας τετραγωνικός πίνακας λέγεται τριγωνικός άνω, όταν όλα τα στοιχεία του που βρίσκονται κάτω από την κύρια διαγώνιο είναι μηδενικά και τριγωνικός κάτω, όταν όλα τα στοιχεία του που βρίσκονται πάνω από την κύρια διαγώνιο είναι μηδενικά.
Πολλαπλασιασμός Πινάκων | Matrix Multiplication
Αν Α = [α ik ] είναι ένας πίνακας μ x ν και B = [β kj ] είναι ένας ν x ρ πίνακας, τότε ορίζουμε ως γινόμενο του πίνακα Α με τον πίνακα Β και το συμβολίζουμε με A • B ή με ΑΒ τον μ x ρ πίνακα, του οποίου κάθε στοιχείο γij είναι το άθροισμα των γινομένων των ν στοιχείων της i -γραμμής του Α με τα αντίστοιχα ν στοιχεία της j -στήλης του Β. Δηλαδή,
Σχηματικά
![]()
Η χρησιμότητα των πινάκων οφείλεται στον ιδιόμορφο τρόπο με τον οποίο πολλαπλασιάζουμε πίνακες.
Μετά όσα ισχύουν στην πρόσθεση πινάκων και την αφαίρεση πινάκων, θα περίμενε κανείς να ορίσουμε τον πολλαπλασιασμό πινάκων κατά ανάλογο τρόπο με την πρόσθεση, δηλαδή σε δύο πίνακες ίδιων διαστάσεων να πολλαπλασιάζουμε τα αντίστοιχα στοιχεία.
Αν ήταν έτσι, οι πίνακες θα αποτελούσαν απλά «αποθήκες» στοιχείων χωρίς ουσιαστικό λόγο ύπαρξης καθώς δεν θα έκαναν τίποτα περισσότερο από το να ομαδοποιούν πράξεις μεταξύ αριθμών. Ο ορισμός του πολλαπλασιασμού πινάκων είναι λίγο πιο περίπλοκος.
Η προϋπόθεση για τον Πολλαπλασιασμό Πινάκων είναι ότι όσες στήλες έχει ο πίνακας Α τόσες γραμμές έχει ο πίνακας
Β.
Με άλλα λόγια, αν ο Α έχει διαστάσεις m x s, o B πρέπει να έχει διαστάσεις s x n. Τότε το γινόμενο έχει διαστάσεις m x n. Σχηματικά θα λέγαμε για τις διαστάσεις
(m x s) Χ (s x n) = (m x n)
Παράδειγμα πολλαπλασιασμού πινάκων
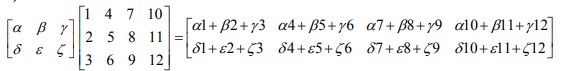
Πολλαπλασιάζουμε δηλαδή την πρώτη γραμμή (α β γ) του πίνακα Α διαδοχικά και με τις 4 στήλες του πίνακα Β. Έτσι προκύπτει η πρώτη γραμμή του ΑΒ. Στη συνέχεια επαναλαμβάνουμε την ίδια διαδικασία με τη δεύτερη γραμμή (δ ε ζ)
Ένα αριθμητικό παράδειγμα πολλαπλασιασμού πινάκων via
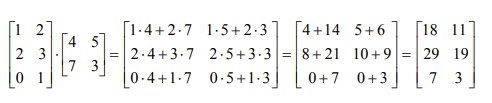
 Ypologismos.gr Life of Numbers
Ypologismos.gr Life of Numbers