Ypologismos.gr Life of Numbers
Υπολόγισε την περίμετρο του τραπεζίου. Άθροισμα μήκους βάσεων και πλευρών τραπεζίου. Τι είναι τραπέζιο; Τα στοιχεία, οι ιδιότητες, οι τύποι του τραπεζίου.
Υπολογισμός μήκους περιμέτρου τραπεζίου online
Perimeter of a trapezium online calculator – calculation
Υπολογισμός περιμέτρου γεωμετρικών σχημάτων – Μπορείτε να υπολογίσετε το μήκος της περιμέτρου ενός τραπέζιου με δύο εναλλακτικούς τρόπους ανάλογα με τα δεδομένα που σας είναι γνωστά :
1 Γνωρίζοντας το μήκος των πλευρών
2 Γνωρίζοντας το μήκος των βάσεων (μικρή & μεγάλη), τις προσκείμενες γωνίες στη μεγάλη βάση και το ύψος
Τραπέζιο – Ευκλείδεια Γεωμετρία
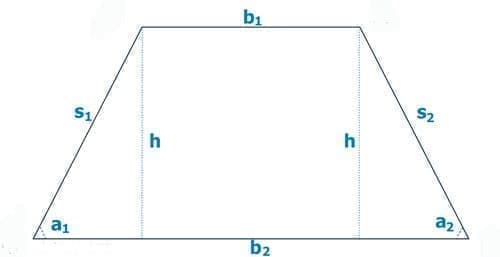
Τραπέζιο στην ευκλείδεια γεωμετρία είναι το κυρτό τετράπλευρο που έχει δύο πλευρές παράλληλες (a, b)
Οι παράλληλες αυτές πλευρές λέγονται βάσεις και η απόστασή τους ύψος (h) του τραπεζίου.
- Ισοσκελές τραπέζιο είναι το τραπέζιο που έχει τις μη παράλληλες πλευρές του ίσες
- Ορθογώνιο τραπέζιο είναι το τραπέζιο που έχει δύο γωνίες ορθές
Μήκος περιμέτρου τραπεζίου – μαθηματικός τύπος
Perimeter of a trapezium – math formula – calculation
Μπορείτε να υπολογίσετε το μήκος της περιμέτρου ενός τραπεζίου, χρησιμοποιώντας τους κάτωθι μαθηματικούς τύπους :
1 Υπολογισμός περιμέτρου τραπεζίου γνωρίζοντας το μήκος των πλευρών
P = b1 + b2 + s1 + s2
και εναλλακτικά επίσης
2 Υπολογισμός περιμέτρου τραπεζίου
γνωρίζοντας το μήκος των βάσεων (μικρή & μεγάλη), τις προσκείμενες γωνίες στη μεγάλη βάση και το ύψος
P = b1 + b2 + h · ( 1/(sin(a1)) + 1/(sin(a2)))
Όπου ισχύει για κάθε παράμετρο του τραπέζιου :
- b1 : Η μικρή βάση (μήκος)
- b2 : Η μεγάλη βάση (μήκος)
- s1 : Η αριστερή πλευρά (μήκος)
- s2 : Η δεξιά πλευρά (μήκος)
- a1 : Η αριστερή γωνία προσκείμενη στην μεγάλη βάση (b2) (σε μοίρες)
- a2 : Η δεξιά γωνία προσκείμενη στην μεγάλη βάση (b2) (σε μοίρες)
- h : Το ύψος του τραπέζιου (μήκος)
- P : Η περιφέρεια (μήκος)
- Α : Το εμβαδόν επιφάνειας (τετραγωνικά)
Τραπέζιο – Ιδιότητες
- Η διάμεσος ενός τραπεζίου είναι παράλληλη προς τις βάσεις του και ίση με το ημιάθροισμά τους.
- Η διάμεσος ενός τραπεζίου διέρχεται από τα μέσα των διαγωνίων του και το τμήμα που αποκόπτεται από αυτές ισούται με την ημιδιαφορά των βάσεων.
