Βρες τον όγκο του ισοσκελούς τριγωνικού πρίσματος online. Υπολόγισε τη χωρητικότητα, τα κυβικά στο ισοσκελές τριγωνικό πρίσμα. Τύπος υπολογισμού. Volume
Ισοσκελές τριγωνικό πρίσμα – Υπολογισμός όγκου πρίσματος
Volume of a Triangular Prism Calculator – Online calculation
Πρίσμα – Γεωμετρία – Στερεομετρία – Γεωμετρικά Στερεά
Τα πρίσματα και οι κύλινδροι μπορούν να προκύψουν με εξώθηση (extrusion) των βάσεών τους κατά h, όπου h το ύψος τους.
Το ανάπτυγμα του πρίσματος είναι ένα ορθογώνιο παραλληλόγραμμο, το οποίο αναδιπλώνεται για να αποδώσει όλα τα επιμέρους ορθογώνια, και οι δύο βάσεις συνδεδεμένες σε μία ακμή τους στις απέναντι πλευρές ενός επιμέρους ορθογωνίου. | via
Ισοσκελές τριγωνικό πρίσμα. Όγκος – Μαθηματικός τύπος
Volume of a isosceles triangular Prism Formula
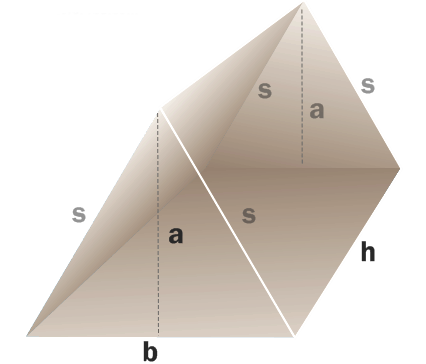
Ο όγκος (V) ενός ισοσκελές τριγωνικού πρίσµατος δίδεται από τον κάτωθι μαθηματικό τύπο :
$$ V = 1/2 · (b · a) · h $$Ορισμός και στοιχεία του πρίσματος
- Βάσεις πρίσματος καλούνται οι τομές των δυο παράλληλων επιπέδων με την πρισματική επιφάνεια
- Παράπλευρες έδρες είναι τα τμήματα των εδρών της πρισματικής επιφάνειας, που περιέχονται μεταξύ των βάσεων
- Παράπλευρες ακμές είναι τα τμήματα των ακμών της πρισματικής επιφάνειας, που περιέχονται μεταξύ των βάσεων.
- Έδρες πρίσματος είναι οι βάσεις και οι παράπλευρες έδρες.
- Ακμές πρίσματος είναι οι πλευρές της βάσης και οι παράπλευρες ακμές.
- Κορυφές πρίσματος είναι οι κορυφές των βάσεων.
- Ύψος πρίσματος είναι η απόσταση των βάσεων.
- Διαγώνιος πρίσματος είναι κάθε ευθύγραμμο τμήμα που τα άκρα του δεν είναι κορυφές της ίδιας έδρας.
- Διαγώνιο επίπεδο πρίσματος είναι κάθε επίπεδο που ορίζεται από δυο παράπλευρες ακμές, που δεν ανήκουν στην ίδια παράπλευρη έδρα
Ειδικές κατηγορίες πρισμάτων
Ορθό καλείται ένα πρίσμα, όταν οι παράπλευρες ακμές είναι κάθετες στις βάσεις.
Κανονικό καλείται ένα πρίσμα, όταν είναι ορθό και επιπλέον οι βάσεις είναι κανονικά πολύγωνα.
Παραλληλεπίπεδο καλείται ένα πρίσμα, όταν οι βάσεις του είναι παραλληλόγραμμα
Μορφές – είδη Πρίσματος
Η ειδικότερη ονομασία ενός πρίσματος προσδιορίζεται από το πλήθος των πλευρών της βάσης. Πενταγωνικό πρίσμα, τριγωνικό πρίσμα, εξαγωνικό πρίσμα κλπ. Από την παραλληλία των βάσεων και την παραλληλία των παράπλευρων ακμών στα πρίσματα προκύπτει
Σε κάθε πρίσμα ισχύουν οι προτάσεις:
- οι παράπλευρες έδρες είναι παραλληλόγραμμα,
- οι παράπλευρες ακμές είναι ίσες,
- οι βάσεις είναι ίσες.
 Ypologismos.gr Life of Numbers
Ypologismos.gr Life of Numbers




