Βρες το ημίτονο μίας γωνίας από τις μοίρες της. Υπολογισμός τριγωνομετρικού αριθμού ημιτόνου online. Ημίτονο σε ορθογώνιο τρίγωνο και σε σύστημα αξόνων
Υπολόγισε το ημίτονο (ημ) μίας γωνίας – Τριγωνομετρικός αριθμός
Sine (sin) of an angle calculator – calculations
Υπολογισμός της τιμής του ημιτόνου μίας γωνίας. Εισάγετε τις μοίρες μίας οποιασδήποτε γωνίας και δείτε πόσο είναι το ημίτονό της καθώς και τη μετατροπή της σε ακτίνια (rad).
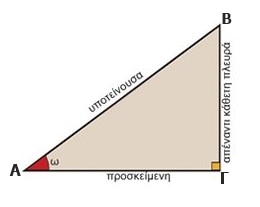
Ημίτονο οξείας γωνίας ορθογωνίου τριγώνου
Σε ένα ορθογώνιο τρίγωνο, ημίτονο ενός εκ των οξειών γωνιών ορίζεται ως το πηλίκο της απέναντι κάθετης πλευράς δια την υποτείνουσα.
π.χ. στο παρακάτω τρίγωνο ισχύει:
Ημίτονο γωνιών από 0° μέχρι και 360°
Γενικεύοντας, μπορούμε να ορίσουμε το ημίτονο οποιασδήποτε γωνίας ω.
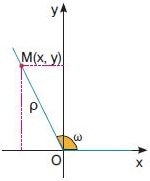
Σε ένα σύστημα συντεταγμένων στο επίπεδο παίρνουμε ένα τυχαίο σημείο Μ με συντεταγμένες Μ(x,y). Φέρνουμε ημιευθεία που ξεκινάει από την αρχή των αξόνων Ο(0,0) και περνάει από το σημείο Μ.
ω είναι η γωνία που σχηματίζεται από τον ημιάξονα Ox αν περιστραφεί κατά τη θετική φορά γύρω από το Ο μέχρι να συμπέσει για πρώτη φορά με την ημιευθεία που σχεδιάσαμε.
Ο ημιάξονας Ox είναι η αρχική πλευρά της γωνίας ω και η ημιευθεία που περνάει από το Μ λέγεται τελική πλευρά της γωνίας ω.
Τότε:
Το ημίτονο της γωνίας ω ισούται με το πηλίκο της τεταγμένης του σημείου Μ με την απόσταση του σημείου από την αρχή των αξόνων.
Δηλαδή, $$ ημω = y/ρ $$
Όπου το ρ είναι η απόσταση της αρχής των αξόνων από το σημείο Μ και με τη χρήση του Πυθαγορείου θεωρήματος βρίσκουμε ότι ισούται με:
$$ ρ = √{x^2 + y^2} $$Ημίτονο για γωνίες μεγαλύτερες από 360°
Οι τριγωνομετρικοί αριθμοί (ημίτονο, συνημίτονο, εφαπτομένη) των γωνιών που είναι μεγαλύτερες από 360° ορίζονται όπως και οι τριγωνομετρικοί αριθμοί γωνιών από 0° μέχρι 360° επειδή έχουν την ίδια τελική πλευρά.
π.χ. η γωνία 390° έχει το ίδιο ημίτονο με τη γωνία των 30° καθώς έχει ολοκληρώσει έναν ολόκληρο κύκλο και έχει καταλήξει εκεί που καταλήγει και η γωνία των 30 μοιρών.
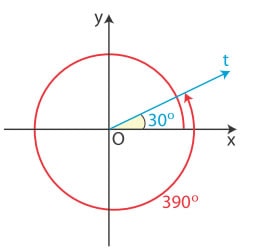
Επομένως διαιρούμε τις μοίρες με το 360 και υπολογίζουμε το ημίτονο του υπολοίπου της διαίρεσης.
Άρα, για κάθε ακέραιο αριθμό k ισχύει: ημ(k*360° + ω) = ημω
Τιμές τριγωνομετρικού αριθμού ημιτόνου
Δηλαδή για το ημίτονο μίας γωνίας ω ισχύει πάντα:
‒1 ≤ ημω ≤ 1
Συνήθεις τιμές ημιτόνου στα Μαθηματικά – Γεωμετρία
Ημ0°, ημ30°, ημ45°, ημ60°, ημ90°, ημ180°
Συνηθίζεται στα μαθηματικά – γεωμετρία να αναζητάμε συχνότερα το ημίτονο των γωνιών των 0, 30, 45, 60, 90 και 180 μοιρών οι οποίες δίνονται παρακάτω:
| 0° | 30° | 45° | 60° | 90° | 180° | |
|---|---|---|---|---|---|---|
| ημω | 0 | $$ 1/2 $$ | $$ √{2}/2 $$ | $$ √{3}/2 $$ | 1 | 0 |
 Ypologismos.gr Life of Numbers
Ypologismos.gr Life of Numbers




