Βρες την εφαπτομένη μίας γωνίας όταν ξέρεις τις μοίρες της. Εύρεση τριγωνομετρικού αριθμού εφαπτομένης. Τι είναι η εφαπτομένη; Πότε δεν ορίζεται; Εύρεση σε ορθογώνιο τρίγωνο και σε σύστημα αξόνων. Μαθηματικοί τύποι
Υπολόγισε την εφαπτομένη (εφ) μίας γωνίας – Τριγωνομετρικός αριθμός
Tangent (tan) of an angle calculator – calculations
Υπολογισμός της τιμής της εφαπτομένης μίας γωνίας. Εισάγετε τις μοίρες μίας οποιασδήποτε γωνίας και δείτε πόσο είναι η εφαπτομένη της καθώς και τη μετατροπή της σε ακτίνια (rad).
Εφαπτομένη οξείας γωνίας ορθογωνίου τριγώνου
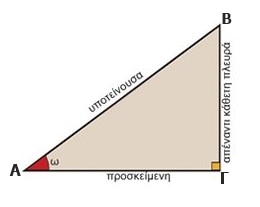
Σε ένα ορθογώνιο τρίγωνο, εφαπτομένη ενός εκ των οξειών γωνιών ορίζεται ως το πηλίκο της απέναντι κάθετης πλευράς δια της προσκείμενης κάθετης πλευράς του.
π.χ. στο παρακάτω τρίγωνο ισχύει:
Εφαπτομένη γωνιών από 0° μέχρι και 360°
Γενικεύοντας, μπορούμε να ορίσουμε την εφαπτομένη μίας οποιασδήποτε γωνίας ω (εκτός συγκεκριμένων μοιρών που αναφέρουμε παρακάτω).
Σε ένα σύστημα συντεταγμένων στο επίπεδο παίρνουμε ένα τυχαίο σημείο Μ με συντεταγμένες Μ(x,y). Φέρνουμε ημιευθεία που ξεκινάει από την αρχή των αξόνων Ο(0,0) και περνάει από το σημείο Μ.
ω είναι η γωνία που σχηματίζεται από τον ημιάξονα Ox αν περιστραφεί κατά τη θετική φορά γύρω από το Ο μέχρι να συμπέσει για πρώτη φορά με την ημιευθεία που σχεδιάσαμε.
Ο ημιάξονας Ox είναι η αρχική πλευρά της γωνίας ω και η ημιευθεία που περνάει από το Μ λέγεται τελική πλευρά της γωνίας ω.
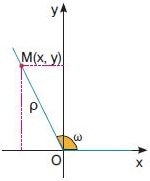
Τότε:
Η εφαπτομένη της γωνίας ω ισούται με το πηλίκο της τεταγμένης του σημείου Μ δια την τετμημένη του σημείου Μ
Δηλαδή, $$ εφω = y/x $$
Εφαπτόμενη για γωνίες μεγαλύτερες από 360°
Οι τριγωνομετρικοί αριθμοί (ημίτονο, συνημίτονο, εφαπτομένη) των γωνιών που είναι μεγαλύτερες από 360° ορίζονται όπως και οι τριγωνομετρικοί αριθμοί γωνιών από 0° μέχρι 360° επειδή έχουν την ίδια τελική πλευρά.
π.χ. η γωνία 390° έχει την ίδια εφαπτομένη με τη γωνία των 30° καθώς έχει ολοκληρώσει έναν ολόκληρο κύκλο και έχει καταλήξει εκεί που καταλήγει και η γωνία των 30 μοιρών.
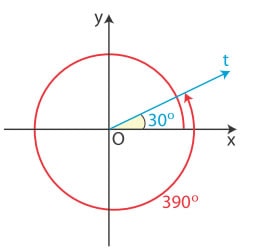
Επομένως διαιρούμε τις μοίρες με το 360 και υπολογίζουμε την εφαπτομένη του υπολοίπου της διαίρεσης.
Άρα, για κάθε ακέραιο αριθμό k ισχύει: εφ(k*360° + ω) = εφω
Μαθηματικός τύπος υπολογισμού εφαπτομένης με ημίτονο και συνημίτονο
Μπορούμε να υπολογίσουμε την εφαπτομένη μίας γωνίας όταν γνωρίζουμε το ημίτονο και το συνημίτονό της ως εξής:
$$ εφω = {ημω}/{συνω} $$ για κάθε γωνία ω.Τιμές τριγωνομετρικού αριθμού εφαπτομένης
Γενικότερα, δεν υπάρχει εφαπτομένη για τις γωνίες (90° + κ*360°) μοιρών και τις γωνίες (270° + κ*360°) με κ ακέραιο αριθμό.
Συνήθεις τιμές εφαπτομένης στα Μαθηματικά – Γεωμετρία
Εφ0°, εφ30°, εφ45°, εφ60°, εφ90°
Συνηθίζεται στα μαθηματικά – γεωμετρία να αναζητάμε συχνότερα η εφαπτομένη των γωνιών των 0, 30, 45, 60 και 90 μοιρών οι οποίες δίνονται παρακάτω:
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| εφω | 0 | $$ √{3}/3 $$ | 1 | $$ √{3} $$ | δεν ορίζεται |
Συνάρτηση TAN στο Excel
Σύνταξη συνάρτησης – function ΤΑΝ στο Εξέλ
TAN(αριθμός)
Η σύνταξη της συνάρτησης TAN περιλαμβάνει τα παρακάτω ορίσματα:
Αριθμός Υποχρεωτικό. Η γωνία σε ακτίνια της οποίας θέλετε την εφαπτομένη.
Εάν το όρισμα είναι σε μοίρες, πρέπει να το πολλαπλασιάσετε επί PI()/180 ή να χρησιμοποιήσετε τη συνάρτηση RADIANS, για να το μετατρέψετε σε ακτίνια.
Παράδειγμα χρήσης της συνάρτησης TAN
Τύπος: TAN(0,785)
Περιγραφή: Επιστρέφει την εφαπτομένη των 0,785 ακτινίων
Αποτέλεσμα: 0,99920
 Ypologismos.gr Life of Numbers
Ypologismos.gr Life of Numbers




